This is a course project for (CMU 15-618: Storage Systems)[https://course.ece.cmu.edu/~ece746/].
Introduction
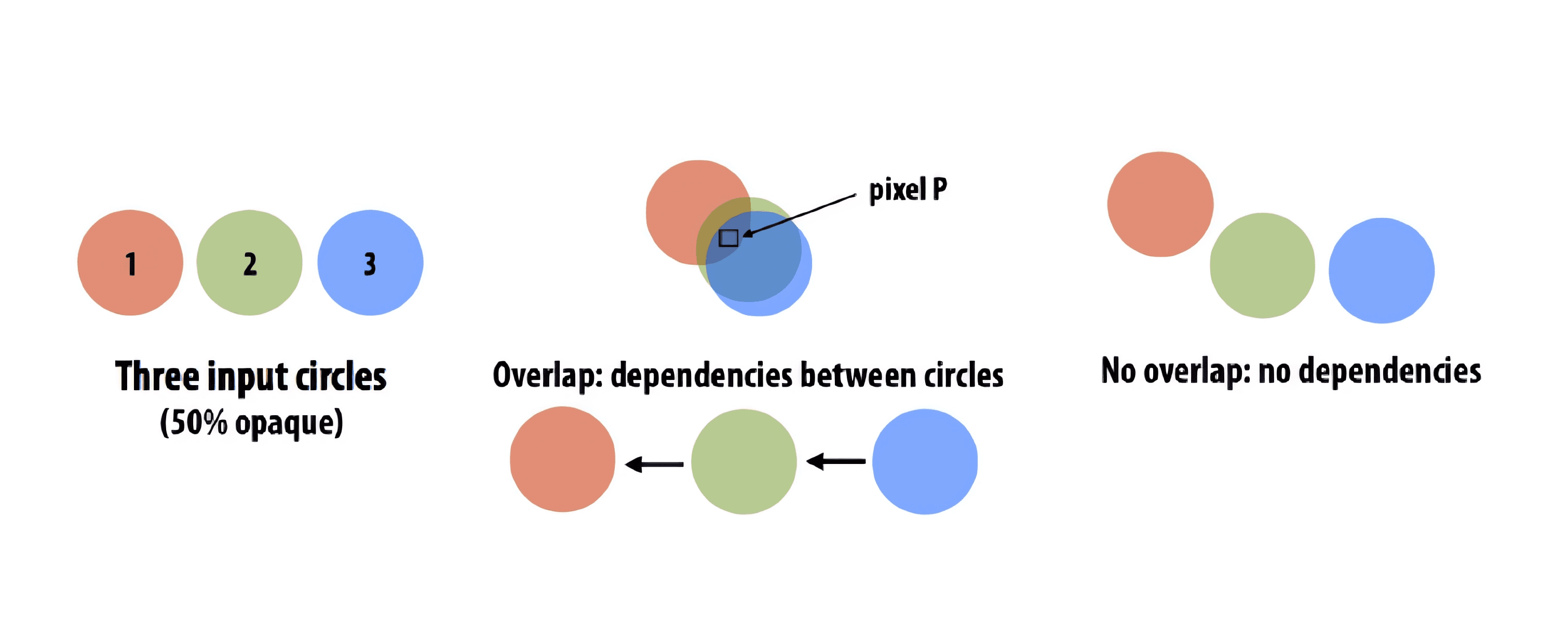
In this project, a parallel image renderer is implemented using CUDA. The renderer takes as input a scene description file and outputs a rendered image. The input files define a scene by specifying the size of the image, the color of the background, and a list of circles. Each circle is defined by its center, radius, color and velocity (the circles will move around in the scene).

The renderer computes the color of each pixel in the image by determining which circles overlap the pixel at runtime and combining the colors of the overlapping circles. It accepts an array of circles (3D position, velocity, radius, color) as input. The basic sequential algorithm for rendering each frame is:
Clear image
For each circle:
Update position and velocity
For each circle:
Compute screen bounding box
For all pixels in bounding box:
Compute pixel center point
If center point is within the circle:
Compute color of circle at point
Blend contribution of circle into image for this pixel
An important detail of the renderer is that it renders semi-transparent circles. Therefore, the color of any one pixel is not the color of a single circle, but the result of blending the contributions of all the semitransparent circles overlapping the pixel (note the “blend contribution” part of the pseudocode above). The renderer represents the color of a circle via a 4-tuple of red (R), green (G), blue (B), and opacity (alpha, written “α”) values (RGBA). Alpha value α = 1.0 corresponds to a fully opaque circle. Alpha value α = 0.0 corresponds to a fully transparent circle. To draw a semi-transparent circle with color (Cr , Cg , Cb , α) on top of a pixel with color Pr , Pg , Pb , the renderer performs the following computation:
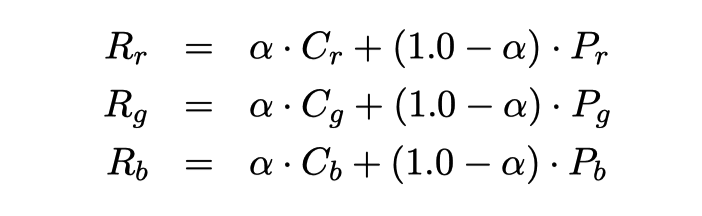
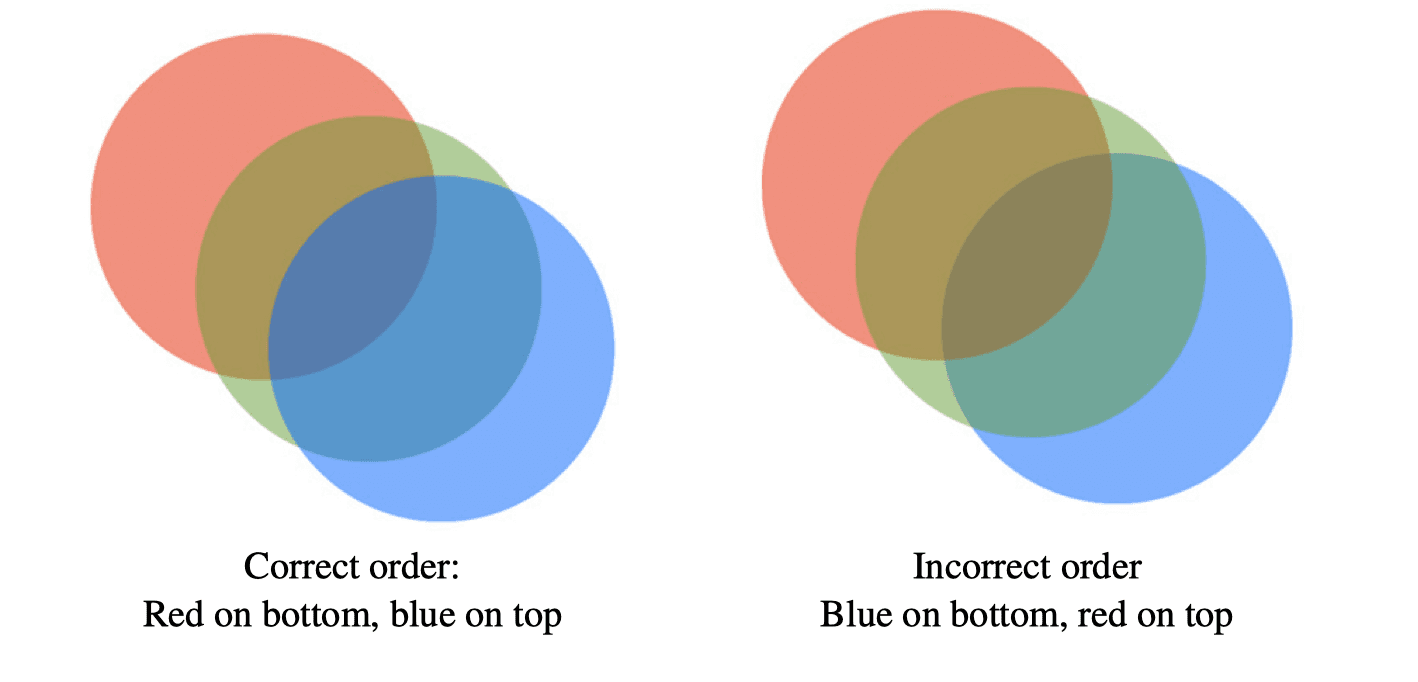
Notice that composition is not commutative (object X over Y does not look the same as object Y over X), so it’s important to render circles in a manner that follows the order they are provided by the application. (You can assume the application provides the circles in depth order.) For example, consider the two images shown in Figure 2, where the circles are ordered as red, green, and blue. The image on the left shows them rendered in the correct order, while the image on the right has them reversed.
Implementation
Below, we will discuss the performance of first three implementations, and provide some data (from nvprof) and intuitions that led us to change our implementation. Then, we will provide a more detailed summary of our final implementation.
Implementation 1: A simple parallel renderer
Our first implementation had two phases. The first set of kernel launches parallelized over blocks of pixels. In other words, one thread corresponded to one 32 by 32 block of pixels (so a block corresponded to a 32 by 32 grid of blocks of 32 by 32 pixels). Then, for every circle and block of blocks pair, one block was launched. Note, since one block was launched for each circle and block of blocks pair, if there were too many circles it was necessary to launch multiple kernels since the z-dimension of the block grid for CUDA is limited to 65535 (https://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html#features-and-technical-specifications).
This first kernel launch was used to compute which circles overlapped each 32 by 32 block of pixels. Specifically, a large amount of memory was allocated with cudaMalloc, and this memory was populated with a mapping that, given a 32 by 32 block of pixels and a circle, could be used to look up if that circle was in the block.
The second kernel launched a block for each 32 by 32 block of pixels in the image. Each thread was assigned to a single pixel in these blocks. This implementation naively stepped through each circle sequentially, checking inclusion in the current block with the mapping populated by the first kernel, and using shadePixel to update the pixels if the circle was within the block.
There were many inefficiencies in this first approach, as displayed by the poor scores in the score table below. One issue was that the code launched approximately 1300 * number of circles blocks for the first kernel (on 1150 by 1150 images). Another issue was that shared memory was not utilized, and the threads were not collaborating. Additionally, the mapping from block-circle pairs to true/false used ints (more memory than was necessary for the information to be stored).
------------
Score table:
------------
-------------------------------------------------------------------------
| Scene Name | Target Time | Your Time | Score |
-------------------------------------------------------------------------
| rgb | 0.1850 | 0.1291 | 12 |
| rand10k | 1.5643 | 25.9128 | 2 |
| rand100k | 14.8853 | 209.7083 | 2 |
| pattern | 0.2860 | 3.1447 | 2 |
| snowsingle | 6.2212 | 208.2952 | 2 |
| biglittle | 11.4153 | 53.4674 | 4 |
-------------------------------------------------------------------------
| | Total score: | 24/72 |
----------------------------------------------------------------------
The relevant portion of the output from “nvprof ./render rand10k -r cuda --bench 0:1” is shown below. This displayed that, for the rand10k render, our renderer was spending the majority of its time in kernelCirclesShade. Note, no additional memory utilization tools were available to us, so nvprof and the score tables were the best ways for us to measure our code’s efficiency.
Overall: 0.0455 sec (note units are seconds)
==83822== Profiling application: ./render rand10k -r cuda --bench 0:1
==83822== Profiling result:
Type Time(%) Time Calls Avg Min Max Name
GPU activities: 90.08% 23.218ms 1 23.218ms 23.218ms 23.218ms kernelCirclesShade(int, int, float, float, int, int, char*)
9.54% 2.4582ms 1 2.4582ms 2.4582ms 2.4582ms kernelCirclesInclusion(float, float, int, int, int, int, char*)
0.20% 52.544us 1 52.544us 52.544us 52.544us kernelClearImage(float, float, float, float)
0.17% 44.865us 9 4.9850us 1.1840us 11.841us [CUDA memcpy HtoD]
Implementation 2: Renderer taking advantage of shared memory
This implementation began to address the issues mentioned in the first implementation. In order to improve collaboration between threads and use of shared memory, as well as to decrease the total number of blocks launched and decrease use of global memory, the blocks and threads were mapped to work in a different way from the first implementation. There were still two kernel launches.
The first kernel launched one block of 32 by 32 threads for each block of 32 by 32 pixels in the image. For each block, the 1024 threads in the block were used to step through the row of the block-circle inclusion mapping for the corresponding block of 32 by 32 pixels. In this way, less blocks were spawned for the first kernel launch (before, there were far too many blocks relative to the number of CUDA cores). Also note, this mapping was changed to store chars instead of ints, which reduced the amount of bytes that needed to be stored/loaded later from global memory.
The second kernel launched one block of 32 by 32 threads for each block of 32 by 32 pixels. The 1024 threads in the block cooperatively loaded 1024 of the circles in the row of the block-circle mapping corresponding to this pixel block. Then, sharedMemExclusiveScan was used to calculate the indices of the circles that were marked as in the block, and the threads wrote the indices of these circles to the beginning of a shared array. Finally, each thread corresponded to one of the pixels, and the circles indices selected above were stepped through for each pixel in order (with calls to shadePixel).
There were still some issues with this approach. One issue was that we were still using cudaMalloc to allocate a very large array in global memory. Then, both of the kernels had many interactions with the global memory. This led to poor performance for the more difficult test cases, as displayed in the score table below.
------------
Score table:
------------
-------------------------------------------------------------------------
| Scene Name | Target Time | Your Time | Score |
-------------------------------------------------------------------------
| rgb | 0.1991 | 0.1750 | 12 |
| rand10k | 1.9623 | 3.2837 | 9 |
| rand100k | 14.7687 | 32.8902 | 7 |
| pattern | 0.2845 | 0.2918 | 12 |
| snowsingle | 7.7129 | 8.9162 | 12 |
| biglittle | 11.7743 | 33.2722 | 6 |
-------------------------------------------------------------------------
| | Total score: | 58/72 |
-------------------------------------------------------------------------
Running nvprof ./render rand10k -r cuda --bench 0:1 indicated that the renderer was still spending the majority of its time in the second kernel. Note, when compared with the last data from nvprof, this data indicates that our improvements to the first implementation were successful.
Overall: 0.0207 sec (note units are seconds)
==84635== Profiling application: ./render rand10k -r cuda --bench 0:1
==84635== Profiling result:
Type Time(%) Time Calls Avg Min Max Name
GPU activities: 91.03% 2.9157ms 1 2.9157ms 2.9157ms 2.9157ms kernelCirclesShade(int, int, float, float, int, int, char*)
5.94% 190.21us 1 190.21us 190.21us 190.21us kernelCirclesInclusion(float, float, int, int, int, char*)
1.63% 52.288us 1 52.288us 52.288us 52.288us kernelClearImage(float, float, float, float)
1.40% 44.832us 9 4.9810us 1.2480us 11.904us [CUDA memcpy HtoD]
Implementation 3: Reducing Global Memory Access
In order to reduce stores/loads to global memory, we merged both of our kernel functions into one kernel. We spawned 1 block of 32 by 32 threads for each block of 32 by 32 pixels. In 1024 chunks of the circle array, the 1024 threads cooperatively loaded the data for the circles, determined if each of these circles was in the block, used sharedMemExclusiveScan to find the indices of the circles that were contained in the block, and wrote these indices to the front of a shared array. Then, each thread corresponded to one of the pixels in the 32 by 32 pixel block, and each thread stepped through the shared array with the relevant circle indices, loading the circle data from global memory and calling shadePixel.
There were still issues with this implementation. Specifically, we did not create a local copy of imagePtr (the pointer to the pixel data in global memory). However, our implementation was drastically improved from the previous version, as displayed in the score table below.
------------
Score table:
------------
-------------------------------------------------------------------------
| Scene Name | Target Time | Your Time | Score |
-------------------------------------------------------------------------
| rgb | 0.1862 | 0.1227 | 12 |
| rand10k | 1.9471 | 2.2303 | 12 |
| rand100k | 15.1151 | 21.5748 | 10 |
| pattern | 0.2704 | 0.2080 | 12 |
| snowsingle | 7.7121 | 4.7711 | 12 |
| biglittle | 13.1609 | 25.3954 | 8 |
-------------------------------------------------------------------------
| | Total score: | 66/72 |
-------------------------------------------------------------------------
Note, the following data, generated using nvprof ./render rand100k -r cuda --bench 0:2, was less helpful than the previous nvprof outputs. Since we condensed all of the work down to one kernel, nvprof tells us that almost all of the time is being spent in this one kernel (which was expected).
Overall: 0.0288 sec (note units are seconds)
==87385== Profiling application: ./render rand100k -r cuda --bench 0:2
==87385== Warning: 1 records have invalid timestamps due to insufficient device buffer space. You can configure the buffer space using the option --device-buffer-size.
==87385== Profiling result:
Type Time(%) Time Calls Avg Min Max Name
GPU activities: 98.49% 28.671ms 1 28.671ms 28.671ms 28.671ms kernelCirclesShade(int, int, float, float, int, int)
1.15% 334.81us 9 37.201us 1.1840us 99.551us [CUDA memcpy HtoD]
0.36% 104.61us 2 52.304us 52.192us 52.416us kernelClearImage(float, float, float, float)
Implementation 4: Final Implementation
The final improvement to our code was to create a local copy of the pixel data from global memory, perform all of the updates on the pixel data, then write it back to global memory at the end (this drastically reduced communication time from global memory access).
Here’s an overview of our render implementation: We first break the input image into square blocks of 32 x 32 pixels geometrically. We have a single kernel function. When we launch this kernel function, we launch 1 block of 32 by 32 threads for each block of 32 by 32 pixels. If the thread corresponds to a pixel that is within the bounds of the image, it loads the initial data for the pixel. Then, we step through the array of circle data in global memory 1024 elements at a time. For each 1024 elements, the 1024 threads in the block collaboratively load the circle data, and each thread computes whether or not the circle that it loaded overlaps the current block. If it does, it marks a value of “1” into a shared array. Then, the 1024 threads collaborate to use sharedMemExclusiveScan to scan this array of “1”s and “0”s, which gives us an index for each circle that overlaps the block. Then, the threads use these indices to write the index of each circle that overlaps the block into another shared array. Then, for each thread that corresponds to a pixel within the bounds of the image, we step through the shared array of the indices of each circle that overlaps the block, the circle data is loaded from global memory, and the pixels are shaded accordingly (with shade pixel). Note, the current pixel data is passed to shadePixel from local memory (not global). Then, the program considers the next block of 1024 circles. After all circles have been processed, if the thread corresponds to a pixel within the bounds of the image, it writes the pixel data that was collected back to global memory.
Note, our implementation maintains atomicity, since only one thread corresponds to each pixel, and it sequentially steps through some subset of the circle indices, updating the pixels one circle at a time. Also, our implementation maintains the circle order, since it considers the circles in 1024 element chunks from the start of the array to the end. Within each of these chunks, it maintains the order of the circles with careful use of scan to gather the relevant circles while maintaining the original order. Then, the pixels are updated in this order (the same as the starting order).
The score table for our final implementation is included below. We ran this code on GHC 67.
------------
Score table:
------------
-------------------------------------------------------------------------
| Scene Name | Target Time | Your Time | Score |
-------------------------------------------------------------------------
| rgb | 0.1865 | 0.1753 | 12 |
| rand10k | 1.9469 | 1.9401 | 12 |
| rand100k | 18.4898 | 18.3768 | 12 |
| pattern | 0.2724 | 0.2465 | 12 |
| snowsingle | 7.7121 | 6.2476 | 12 |
| biglittle | 14.1915 | 16.7866 | 12 |
-------------------------------------------------------------------------
| | Total score: | 72/72 |
-------------------------------------------------------------------------
Note, nvprof ./render rand100k -r cuda --bench 0:1 revealed that, compared to our last implementation, this implementation was significantly faster.
Overall: 0.0354 sec (note units are seconds)
==88283== Profiling application: ./render rand100k -r cuda --bench 0:1
==88283== Profiling result:
Type Time(%) Time Calls Avg Min Max Name
GPU activities: 97.93% 18.317ms 1 18.317ms 18.317ms 18.317ms kernelCirclesShade(int, int)
1.80% 336.00us 9 37.333us 1.2160us 100.16us [CUDA memcpy HtoD]
0.27% 50.848us 1 50.848us 50.848us 50.848us kernelClearImage(float, float, float, float)
To reiterate, the problem was decomposed as follows: each CUDA block was assigned to one 32 by 32 pixel square block in the image. Then, each CUDA thread within the blocks was assigned to work in two ways. First, each thread corresponded to one of the circles in the circle array, and it computed whether or not the circle overlapped with the current block. Then, each thread collaborated to scan the elements in this array. Next, each thread that corresponded to one of the overlapping circles used the index generated by the scan to write the circle index to the shared array. Then, each thread corresponded to a pixel, and it stepped through this shared array, loading the relevant circle data, and shading its pixel accordingly. Note, the scan code, which was provided, decomposed the scan over warps.
There are two places that synchronization occurs in our code. Both of them occur within the kernel function in our implementation. All of the synchronization occurred within the while loop of the code. After all of the circle data was loaded, processed for inclusion, the first point of synchronization occurs with several calls to __syncthreads() within the sharedMemExclusiveScan function provided to us. No synchronization was required before the call to sharedMemExclusiveScan because we know that the code is executed in warps (__syncthreads() happens after the warp scan, which is okay because all of the necessary data will have been loaded by each warp of threads). The second point of synchronization is after the threads have written the indices of the circles within the current block to the array in shared memory. This is needed to prevent threads from beginning to shade pixels without the full data on the circles in the block.
We reduced communication requirements due to synchronization in several ways. First, by condensing down to one kernel, we removed a call to cudaDeviceSynchronize(). Second, by carefully reasoning about sharedMemExclusiveScan (as described above) we were able to removed redundant calls to __syncthreads(). Finally, we were able to remove a call to __syncthreads() at the end of the while loop. We noticed that, after the last point of synchronization, the threads needed access to the last value of the input and output array to the scan, as well as the shared array of circle indices to evaluate. We also noticed that only the input array to the scan could possibly be modified before the next point of synchronization. As such, we wrote some additional code to copy the last value of the input array to scan into shared memory before a synchronization point. This allowed us to remove the call to __syncthreads() at the end of the while loop.
We took several steps to reduce communication requirements by eliminating unnecessary global memory accesses. The first step we did is that we compact the two kernel functions we used in our first implementation into one. By doing that, we no long need to allocate global memories for the two kernel functions to communicate with each other. Instead, we utilized per-block shared memory to store the circle intersection results and then shading logic can access the data without bothering requesting data from the global memory.
The second communication optimization we made is that we load the pixel data into per-thread local memories/registers first, and write the pixel data back only when we are done computing all the circles’ contribution to it. This approach speeds up our render considerably and leads to a full score.